Quantum Mechanics 2
1. Wave Function
the schrodinger equation is given by
where the reduced planck constant is
is the area under the graph of
However we see that from the schrodinger equation above if
suppose that the wave function is normalized at some time say
we may differentiate under the integral like so(since
next see that
Now the Schrödinger equation says that
and hence also (taking the complex conjugate of above)
so
The integral can now be evaluated explicitly:
and obviously necessary condition is that we must have
as desired
momentum
for a particle in state
now consider
which simplifies to
via integration by parts specifically using
where
upon rearrangement we then define the expectation value of momentum by
finally we write out expectation values
the terms in the brackets are operators which basically takes a function and then spits out another function. In our case
we say that:
represents the position operator (multiplies by ) represents the momentum operator (differentiate w.r.t then scale by
in fact we may generalize this to represent any operator knowing from classical mechanics that any dynamical variable can be expressed in terms of position and momentum
The expectation of kinetic energy is
2. Time independent schrodinger equation
stationary states
consider the schrodinger equation again
we now look for solutions of the form
through a method of PDE solving known as separation of variables
then we substitute it into the equation to obtain
after dividing by
so it is apparent by basic ODE knowledge that
and
or
the latter equation is known as the time independent schrodinger equation
what is the benefit of separable solutions?
- They are stationary states
eg. the expectaion value of any dynamical value is constant in time - They are states of definite total energy
that is, every measurement of total energy is certain to return the value E. To see how so consider the
hamiltonian defined by
and its associated hamiltonian operator defined by
so that our time independent schrodinger equation can be rewritten as
To show certainty we calculate the variance of H. To that end we first calculate its expecation
where we note that we assume normalization of
since
so clearly we have zero variance as seen in
prove the following three theorems:
-
For normalizable solutions, the separation constant
must be real. Hint: Write (in Equation 2.7) as (with and real), and show that if Equation 1.20 is to hold for all , must be zero. -
The time-independent wave function
can always be taken to be real (unlike , which is necessarily complex). This doesn't mean that every solution to the time-independent Schrödinger equation is real; what it says is that if you've got one that is not, it can always be expressed as a linear combination of solutions (with the same energy) that are. So you might as well stick to s that are real. Hint: If satisfies Equation 2.5, for a given , so too does its complex conjugate, and hence also the real linear combinations and . -
If
is an even function (that is, ) then can always be taken to be either even or odd. Hint: If satisfies Equation 2.5, for a given , so too does , and hence also the even and odd linear combinations .
2.3 The Harmonic Oscillator
from Hook's law we get
where
so subbing
Algebraic Method
first we rewrite the above as
where
Next we define the ladder operator
now see that
notice the last bracketed term is the form we define as the commutator of
so in our case this term is
so we have
we call this formula the canonical commutation relation so returning to the above we have
or
However the order of such a product matters as consider
notice that
in which case we have
therefore
in particular we have essentially arrived at the following results
and so plugging this into our time independent schrodinger equation we have
If
proof: consider
similarly we have
proof consider
essentially we not have a ladder of states for the harmonic oscillator where the ladder operators
so what is the lowest possible energy? Surely we can't possibly keep moving down the ladder. To that end we define the "lowest rung of the ladder" by
by definition of ladder operators and that
solving this using usual DE methods we have
so we have
normalizing this(recall we mentioned
so
now recall the formula for time indepedent shrodinger equation with our ladder operators we now have
and given the boundary condition
now recalling ladder of states we have that
and that
furthermore plugging this into our time independent schrodinger equation
we get
alternatively we also have
from these it is clear to see that we have
for any
in the langauge of linear algebra
proof: by integration by parts (with vanishing boundary terms) shows that
but
Under the usual assumptions (wavefunctions vanish at infinity), the boundary term
Therefore
where we had
now comes the whole point of the ladder operators. We seek to find
where we seek to find the constants
so therefore we conclude that
and we also immediately see that
we have
i.e we the stationary states are orthogonal
proof Consider using this relation from before we have
but at the same time we may use the hermitian property of ladder operators above to shift the ladder operators twice so they all act on the
so we now have
clearly
Find the expectation value of the potential energy in the nth stationary state of the harmonic oscillator
solution: first by definition we will have
which is basically using the standard expectation of operator form from previously which expresses in terms of the position and momentum operator
First using definition of ladder operators we rearrange to obtain
Next because we are interested
and then sub it back into
now
2.4 The free particle
Consider the case where
or
in which case case from our knowledge of basic ODE we know that our solution is in the form
now recalling the stationary state solution form of the full wave function
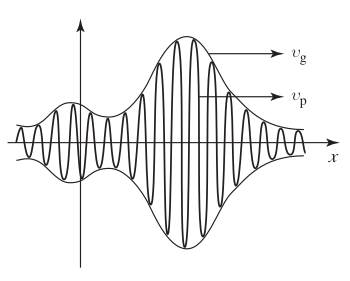
now the first term represents a wave travelling to the right while the second to the left. We denote each term by
with
which in contrast to the classical speed of free particle with energy E(since
so apparently the quantum mechanical wave function travels at half the speed of the particle it is supposed to represent?!
an even bigger problem is that the wave function is not normalizable! just consider
This means
- there is no such thing as free particle with definite energy
- the wave solution is not separable for a free particle
Instead if we allow for
- a range of
and thus a range of associated energies - the wave function to be a superposition of individually separable solutions for each
Specifically
note although invidually separable, the overall superposition itself is not seperable as you cannot factorize the whole superposition itself
then finally unlike before this solution can be normalized for appropriate
now suppose we are given the initial conditions
we use the plancherel theorem(recall Functional Analysis) where we have in our case
Now that we have established that finding a separable solution
we have
proof: First start with
where
then do a change of variables from
2.5 The Delta Function Potential
to summarize so far for the time-independent schrodinger equation we have:
- for the infinite square well and harmonic oscillator they are normalizable and labelled by a discrete index n
- for the free particle they are non-normalizable and are labnled by the continuous variable k
So you might ask what is the significance of this?
In classical mechanics a one-dimensional time independent can give rise to two different kinds of motion. If
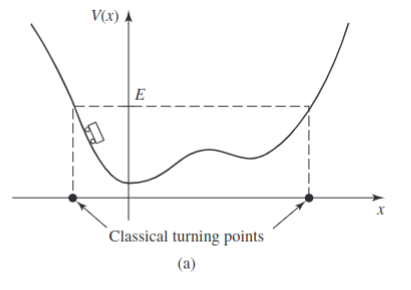
On the other hand
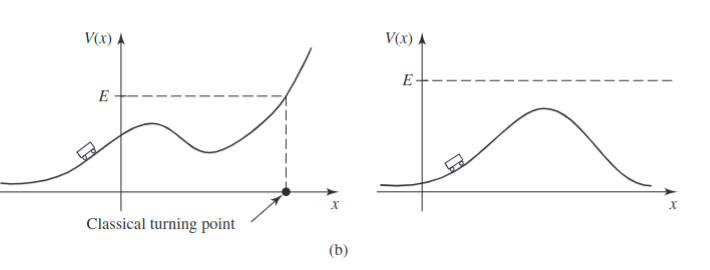
It turns out that the 2 kinds of solutions to the Schrodinger equation as mentioned above correspond precisely to bound and scattering states. Specifically
In real life most potentials go to zero at infinity in which case the criterion simplifies to
The Delta Function Well
The dirac delta function is an infinitely high infinitesimally narrow spike at the origin whose area is
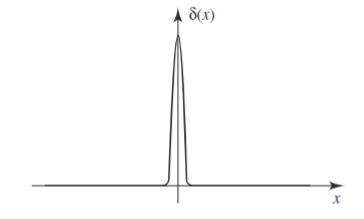
In fact the dirac delta function isn't a function at. The above is just an approximation, in reality the dirac delta function is just a straight line up essentially. Basic high school calculus vertical line test already tells you this can't be a function! More specifically this is a distribution(refer to Distribution Theory and Fourier Analysis for more information)
Let us now consider a potential of the form
So plugging this into the time independent schrodinger equation we have
it yields both bound states(
In the region
where
since
as usual. Now because the first term blows up as
in the region
Now we first assume the standard conditions for
is always continuous is continuous except at points where the potential is infinite
therefore combining the combining the above 2 relations we must have
which is clearly continuous. Next also see that 2 is indeed satisfied. To see consider the limit
then we have
since the last integral is zero as
from here we also see that the delta function determines the discontinuity in
where from the definition of
therefore we get another expression for the discontinuity
therefore subbing our expressing for
What is the fourier transform of
solution: first do as instructed
then simply take the inverse fourier transform to get back
yielding the result as desired
show that
solution: Consider the integral,
Assuming that c is positive, make the following substitution.
Consequently,
Make the same substitution again, this time assuming that c is negative.
Now combine these results.
Therefore,
3. Formalism
3.1 Hilbert Space
Quantum theory is based on two constructs: wave functions and operators. The state of a system is represented by its wave function, observables are represented by operators.
To represent a possible physical state as we know the wave function must be normalized
The set of all square-integrable functions on a specific interval is defined by
or basically the
in particular we are saying that wave functions live in the hilbert space
The inner product of two functions is written as
this also means that
we also have that the inner product with itself
is real and non-negative; it's zero only when
The function is said to be normalized if its inner product with itself is 1 and two functions are orthogonal if their inner product is zero and a set of functions
Finally a a set of functions is complete if any other function(in Hilbert space) can be expressed as a linear combination of them
If the functions
3.2 Observables
3.2.1 Hermitian Operators
the expectation value of an observa le
The outcome of a measurement(observable) must be real and so therefore we must have
For this to happen we must have by definition of expectation value:
specifically they must have a property where
we call such operators hermitian.
To emphasize we are essentially saying that observables are represented by hermitian operators(as they must be real)
let us verify this
Consider the momentum operator. Let us check if it is hermitian
The hermitian conjugate(or adjoint) of an operator
note: we are referring to the transpose conjugate specifically hence the above relation
that is a hermitian operator is then equal to its hermitian conjugate
Show that if
Solution:
Suppose that
and
- (a) Show that the sum of two hermitian operators is hermitian.
- (b) Suppose
is hermitian, and is a complex number. Under what condition (on ) is hermitian? - (c) When is the product of two hermitian operators hermitian?
- (d) Show that the position operator
and the Hamiltonian operator are hermitian.
3.2.2 Determinate States
normally when you measure an observable
Formally this means the variance of
where we have the final relation because since
this is basically the eigenvalue equation for the operator
To sum up essentially we say that:
Determinate states of Q are eigenfunctions of
We also say that the collection of all eigenvalues of an operator is called its spectrum and if 2 or more linearly independent eigenfunctions share the same eigenvalue we say such a spectrum is degenerate
3.3 Eigenfunctions of Hermitian Operator
we now turn our attention to eigenfunction of hermitian operators, physically that refers to determinate states of observables if you recall
- if the spectrum is discrete then the eigenfunctions lie in the Hilbert Space
- if the spectrum if continuous then the eigenfunctions are not normalizable
recall the for free particle where we have continuous spectrum, we did not have normalizable eigenfunction unless we considered a "packet". This is in contrast to that of the simple harmonic oscillator which has a discrete spectrum related by ladder operators.
3.3.1 Discrete Spectra
their eigenvalues are real
proof suppose
since
then recall first slot of inner product is conjugate linear so
the eigenfunctions belonging to distinct eigenvalus are orthogonal
Proof: Suppose
and
(again, the inner products exist because the eigenfunctions are in Hilbert space). But
the eigenfunctions of an observable operator are complete, that is any function in the hilbert space can be expressed as a linear combination of them. This is taken as an axiom in quantum mechanics
more precisely this is done by rtestricting the class of hermitian operators that can represent observables
3.3.2 Continuous Spectra
(a) Cite a Hamiltonian from Chapter 2 (other than the harmonic oscillator) that has only a discrete spectrum.
(b) Cite a Hamiltonian from Chapter 2 (other than the free particle) that has only a continuous spectrum.
(c) Cite a Hamiltonian from Chapter 2 (other than the finite square well) that has both a discrete and a continuous part to its spectrum.
Find the eigenfunctions and eigenvalues of the momentum operator on the interval
solution: Let
This is a standard constant coefficient ODE with general solution
immediately we see this is the same situation as the free particle case(see above). We know this is not normalizable hence the momentum operator has no eigenfunctions in Hilbert space(i.e the square integrable or
If we pick
then
Which is reminisicent of true orthonormality. Basically instead of kronecker delta we have dirac delta. This is known as dirac orthonormality. With this, as usual as physicts we assume that eigenfunctions with real eigenvalues are complete so we have
for any square integrable function
Similarly find the eigenfunctions and eigenvalues of the position operator
solution: Let
see that
just like above we then know that such eigenfunction are not square integrable but rather are Dirac orthonormal
3.4 Generalized statistical Interpretation
Quick recap basics first. Recall that eigenfunctions of an observable operator are complete that is
and because the eigenfunctions are orthonormal we have
proof consider
where recall from the start that we must have
Similarly we have
proof: Consider
but